Parmenides’in öğrencisi Zenon, Aristo’nun diyalektik düşünce dediği, karşıdakinin fikirleri hakkında mantık çerçevesinde yorumlama yapmasıyla biliniyordu. Parmenides ise şu şekilde düşünüyordu: Her şey “bir” türlüdür, değişmez. Algıladığımız dünyada olan şeyler — çokluk, değişim, hareket… — duyu organlarımızın bir oyunudur.

Zenon yaşadığı dönemde (MÖ 334 — MÖ 262) sonsuzluk fikri sezgiye çok ters durumlara yol açıyordu. Bu şaşırtıcı yorumları yapan Zenon, “Zenon Paradoksları” ile tanınmış oldu. Zenon’un ortaya attığı paradokslar hocasının fikirlerini destekler nitelikteydi. Zenon Paradoksları güzel bir irdeleme örneğiydi ve zararsızdı çünkü sonsuzluk kavramının daha iyi anlaşılmasıyla çoğu sorun ortadan kalktı. Hadi şimdi bu faydalı paradoksların 3 tanesine bir göz atalım.

1. Paradoks: Aşil ile Kaplumbağa

Aşil ile kaplumbağa bir yarışa girişmişler. Aşil, kaplumbağaya bir şans tanıyarak önden başlamasına izin vermiş. Zenon, Aşil’in kaplumbağaya hiçbir zaman yetişemeyeceğini ileri sürmüştü.

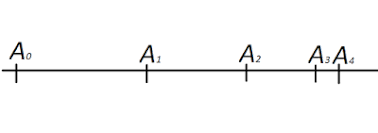
Aşil A(0), kaplumbağa ise A(1) noktasında olsun. Aşil’in kaplumbağayı yakalaması için önce A(1) noktasına gelmesi gerekir bu zaman zarfında kaplumbağa sürekli hareket edeceği için başka bir A(2) noktasına ulaşır. Şimdi de Aşil’in A(2) noktasına gelmesi gerekecektir. Bu sırada kaplumbağa A(3) noktasına varır. Şimdi Aşil A(3)’e varmak zorunda… Bu böyle sürüp gider ve Aşil kaplumbağayı hiçbir zaman yakalayamaz.

Zenon ve Parmenidus ve diğer filozoflar — en azından çoğu — Aşil’in kaplumbağayı gerçek hayatta geçeceğini biliyorlardı fakat bu yöntemdeki mantık hatası neydi? Bir hata var mıydı? Bir örnekle durumu somutlaştırmaya çalışalım. Diyelim ki Aşil saniyede 100 metre, kaplumbağa saniyede 10 metre koşsun. Aşil’in kaplumbağayı yakalayabilirse kaç saniyede yakalayabileceğini bulmaya çalışalım. Aşil A(n)’den A(n+1)’e gidene kadar geçen süreye T(n+1) diyelim. Aradığımız şey : T(1) + T(2) + T(3) + T(4) + … = T

Hesaplar kolay olsun diye aradaki mesafe de 100 metre olsun. Aşil A(1)’e 1 saniyede varır. T(1) = 1 sn. Bu 1 saniyede kaplumbağa 10 metre yol alır ve A(2)’ye ulaşır. Aşil A(2)’ye 1/10 saniyede ulaşır. T = 1/10 sn. Bu 1/10 saniyede kaplumbağa 1 metre yol alır ve A(3)’e ulaşır. Aşil A(3)’e 1/100 saniyede ulaşır. T(3) = 1/100. Bu böyle gider. Yani,

T = 1 + 1/10 + 1/100 + 1/1000 + 1/10000 + … = 10/9

Neden böyle olduğunu çok nitelikli bir yöntem olmasa da şu şekilde anlatalım.

T = 1 + 1/10 + 1/100 + … T’yi 10 la çarpalım.

10T = 10 + 1 + 1/10 + 1/100 + … Üsttekini alttakinden çıkaralım.

9T = 10 gelir. Buradan T = 10/9 çıkar.

Aslında tam olarak çıkmaz… Ancak, T’nin sonlu bir sayı olduğunu biliyorsak 10/9 çıkar. Örneğin A = 1 + 2+ 4+ 8 + … olsun. A’nın sonlu olmadığı besbellidir. A’yı 2 ile çarpalım. 2A = 2 + 4 + 8 + 16 + … = A-1 olur. Buradan A = -1 gibi saçma bir sonuç çıkar.

Bu durumda belirlediğimiz T sayısının sonlu bir sayı olduğu konusunda bu yazı boyunca bana güvenin ve T = 10/9 olduğunu anlamaya çalışın.

Kısacası, bizim hesabımıza göre Aşil kurbağayı 2 saniyeden az bir süre içinde yakalar. Felsefeciler de bu sonsuz toplamların sonucunun sonlu bir sayı çıkmasına bir şey demiyorlar ama bu sonsuz toplam işini gerçek dünyaya uygulamaya gelince çoğu insanın tadı kaçar. Çünkü mantığa ters düşen kısım şu : “Nasıl iş sayısı sonlu olmaz ve bu işleri sonlu sürede yapabilirsin?”

2. Paradoks: Hiç bitmeyen yol!

Şimdi kaplumbağayı atalım ve sadece Aşil’e odaklanalım. Aşil yarışı bitirebilir mi? Önce yarısını gitsin sonra kalan yolun yarısını sonra kalan çeyrek yolun yarısını sonra onun da yarısını… Bu hep böyle devam ederse bu yol biter mi yahu! Tersten düşünürsek de daha garip bir sonuç çıkıyor. Yarışı bitirebilmesi için önce yolun yarısını gitmeli.

Yolun yarısına varabilmek için önce 1/4’ünü gitmeli. Yolun çeyreğine varabilmesi için önce yolun 1/8’ini gitmeli, ondan önce 1/16’sını gitmeli … Bu böyle giderse bir adım bile atamaz ki. Her hareketi için önce o hareketin yarısını yapmalı. Her mesafenin de yarısı varsa… Aşil hareket edemiyor o zaman. Ama pratikte hareket eder. O halde daha fazla bölünemeyen bir birim mi var? Yol n sayıda adımda bitse alınan yolu hesaplamak biliniyordu.

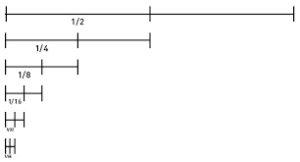
1 + 1/2 + 1/4 + … + 1/2^^n =[(1/2)^^(n+1)-1]/(1/2–1) = 2–1/2^^n

Fakat bu gösterimden şu gösterime geçiş yapamamışlardı.

1 + 1/2 + 1/4 + … = 1/(1–1/2) = 2

3. Paradoks: Havaya Atılan Ok

Zenon’un 3. paradoksu hiçbir şeyin hareket etmediğini öne sürüyordu.

Oktan yola çıkarak Zenon’un ne demek istediğini anlamaya çalışalım. Bir oku havaya fırlattığınızda gideceği yolu parsellere bölelim. Önce 1. parçayı gidecek. Biz 1. parçayı da parçalayalım. Çok daha kısa süre içinde 1. parçanın 1. parçasını gitmeli. Bu süreden daha kısa süre içinde 1. parçanın 1. parçasının 1. parçasını gitmeli. Bundan çok çok daha kısa süre içinde de … Bu böyle gider. Fotoğraf makinesiyle okun fotoğrafını çektiğinizde oku hareket eder şekilde değil, durmuş halde görürsünüz. Bu durumda duyularımız bizi yanılttı mı?

Gerçek hayatta; tavşan kaplumbağayı geçer, ok havada hareket eder ve biz A noktasından B noktasına ulaşırız. Peki bunu matematiğe dökmeye çalışınca neden böyle oluyor? Aslında pek bir sıkıntı çıktığı söylenemez. Bu sıkıntılar limit ve yakınsama gibi kavramlarla halledildi. Sadece Zenon döneminde sonsuz toplamlar, yakınsamak, limit alma gibi fikirler oturmadığı için bu şekilde şaşırtıcı olaylar ortaya çıkmıştı. Zenon’un paradoksları matematiğin gelişmesine katkıda bulundu mu? Evet. Matematik evreni ve kurduğumuz düzeni anlamlandırma çabamızda kullandığımız bir araç. Genellikle bu yüzden teori ile pratiğin uyuşmasını bekleriz. Teori ile pratik uyuşmadığında ise teori tekrar gözden geçirilir.

Ceren Şahin

Kaynaklar,

1. Mackenzie, Dana. The Story of Mathematics in 24 Equations. İstanbul: Ketebe Kitap ve Dergi,2019.
2. Nesin, Ali. Zenon Paradoksları.alinesin.org. Web.23.01.2020.